How to Find a Basis for a Nullspace
For easier method I recommend observation directly. Since the linear combination equation has only the zero solution the vectors 1 1 0 0 0 1 are linearly independent.

Example Of Basis For A Null Space Youtube
A-BABA2-B2 for Matrices A and B The Matrix for the Linear Transformation of the Reflection Across a Line in the Plane.

. A u 0 The Null space of a matrix is a basis for the solution set of a homogeneous linear system that can then be described as a homogeneous matrix equation. How does Null Space Calculator Works. A null space is also relevant to representing the solution set of a general linear system.
1 2 1 0 1. 1 The null space of A consists of all vectors of the form bf x above. What is a Basis.
The Null Space Calculator will find a basis for the null space of a matrix for you and show all steps in the process along the way. The null space and the row space are in the input space while the column is in the output space. More precisely to find a basis for the null space begin by identifying the leading variables xℓ1xℓ2xℓr where r is the number of leading vari-ables and the free variables xf1xf2xfnr.
The row and the column space have the same vectors in the basis same dimension. Ns nullAr When I look at the source code I saw that it is calculated like. 2 The dimension of the null space is 3.
If you want to find nullspace of matrix for random values then click on the generate matrix. A Find a basis for the nullspace of. Since the length of the basis vector is 12 02 12 2 it is not orthonormal basis.
R 1 1 0 0 0 0 1 1 Find the columns that dont have leading entries in this case the second and last. First you transpose the matrix A then you do row elimination to find pivot columns and free columns. In general if A is in RREF then a basis for the nullspace of A can be built up by doing the following.
To get a basis for the null space you can use the constant vectors in the right hand side. Basis for nullspace of A A A A1. Algebra questions and answers.
Nullspace of a matrix is to use row-reduction. 1 0 1 is a basis of the null space of A. You know the usual way to find the basis for the left nullspace NAT.
C Find a basis for the range of that consists of column vectors of. The dimension of the null space comes up in the rank theorem which posits that the rank of a matrix is the difference between the dimension of the null space and the number of columns. The null space and the row space are dual in in the input space.
Null space of a matrix A Written Null A is. We use reduced row echelon form to assign dependen. I am trying to calculate the rational basis for null space of a matrix.
Find the n r solutions to Ux 0 corresponding to the free-. Enter the size of rows and columns of a matrix and substitute the given values in all fields. B Find a basis for the row space of.
3 We need three independent vectors for our basis for the null space. An online nullspace calculator can find a basis for the null space of the matrix by following these steps. One way to find a basis for the kernel aka.
Row-reducing A T goes pretty quickly since there are only two rows producing. The resulting solution will give a. Click here if solved 32.
Then you set free variables then find pivot variables. This means the combination of the basis of the null space and the row space is the basis of the input space. For each free variable set it to 1 and the rest of the free variables to zero and solve for the pivot variables.
Add to solve later. Rank A dim Col A dim Nul A displaystyle operatorname Rank Aoperatorname dim operatorname Col A-operatorname dim operatorname Nul A. Find a basis for the null space of the matrix A 1 0 3 2 1 0 2 2 4 4 0 0 0 2 6.
Thus we divide the vector by its length and obtain an orthonormal basis. Find a basis for the subspace of Find 3. X x3 0 x3 x3 1 0 1.
Find a basis for the Null Space and a basis for the Column Space of A 1 3 2 5 1 3 2 6. Therefore the set 1 1 0 0 0 1 is a linearly independent spanning set thus it is a basis for the null space N A. D For each column vector which is not a basis vector that you obtained in part c express it as a linear combination of the basis vectors for the range of.
By definition any vector in the null space is a linear combination of the above three vectors. Find a basis for the Null Space and a basis for the Column Space of A 1 3 2 5 1 3 2 6. Comments and suggestions encouraged at email protected.
We have to find the basis for nullspce of A and basis for the column space of A a we have to find basis for the nullspace of A To find the basis for the nullspace of A solve the system Ax 0 where Augmented matrix is given by so View the full answer. For the free variables let tj xf j. Its the same way to find the null space of A.
So what we can do is take bf x and split it up as follows. How to Find a Basis for the Nullspace Row Space and Range of a Matrix True or False. Here is how this is done in MATLAB.
Ing a homogeneous system Ax 0 results in a basis for the null space. And it is easy to see that the three are linearly independent. There is quite a few posts about how nullspace is calculated using Pythonnumpy but they calculate it for orthonormal basis and not for the rational basis.

Linear Algebra Example Problems Null Space Example 2 Youtube

How To Compute The The Basis Of The Null Space In Maple Mathematics Stack Exchange
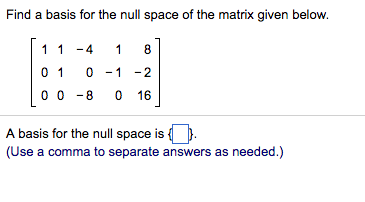
Solved Find A Basis For The Null Space Of The Matrix Given Chegg Com

Find The Null Space Of A Matrix Youtube

Null Space Of A Matrix Youtube

Find The Null Space Of A Matrix Youtube

Linear Algebra Finding A Basis For The Null Space Of A Matrix R Learnmath
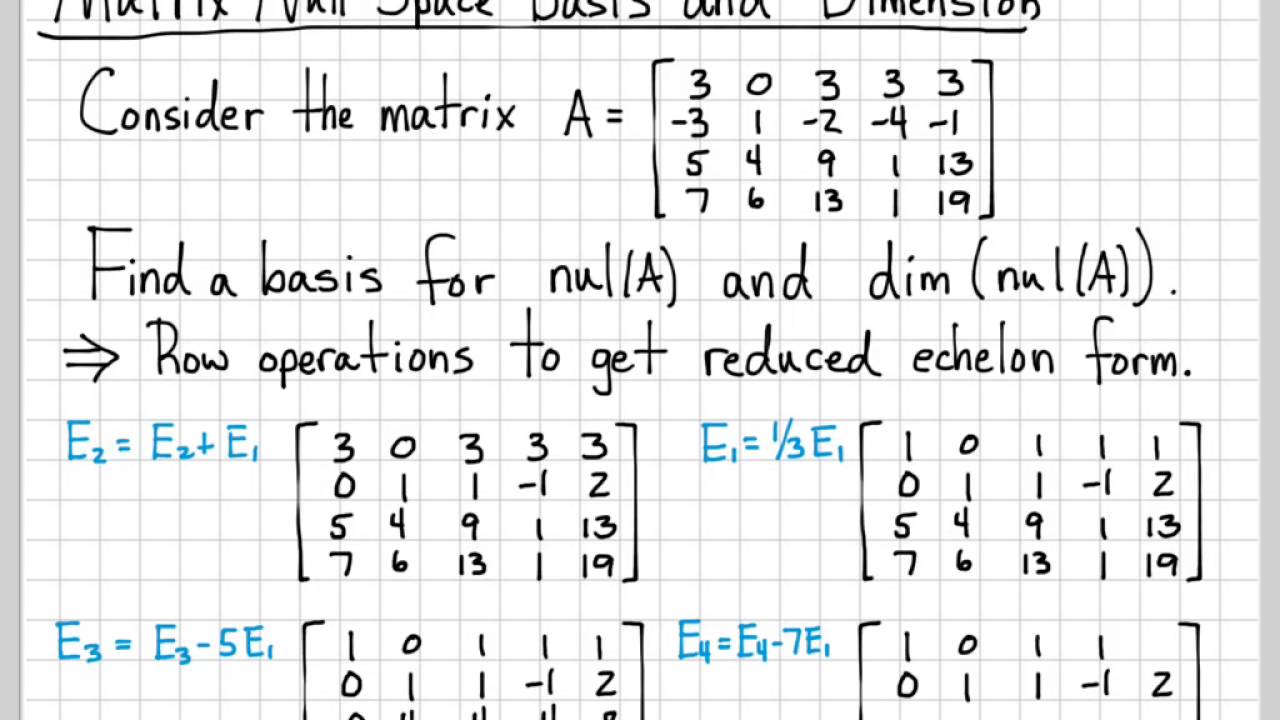
Linear Algebra Example Problems Matrix Null Space Basis And Dimension Youtube

Linear Algebra Finding The Rank And Basis Of Null Space Of This Matrix Mathematics Stack Exchange
Comments
Post a Comment